Mô men quán tính là một đại lượng vật lý quan trọng trong lĩnh vực cơ học, đặc biệt là trong chuyển động quay. Nó mô tả khả năng chống lại sự thay đổi vận tốc góc của một vật. Bài viết này sẽ giải thích chi tiết về mô men quán tính, công thức tính trong các trường hợp khác nhau và ứng dụng thực tế của nó, đặc biệt liên quan đến [keyword].
Mở đầu
Trong chuyển động thẳng, khối lượng là đại lượng biểu thị mức độ quán tính của vật, tức là khả năng chống lại sự thay đổi vận tốc. Tương tự, trong chuyển động quay, mô men quán tính đóng vai trò tương đương. Nó phụ thuộc vào sự phân bố khối lượng của vật thể và vị trí của trục quay. Hiểu rõ về mô men quán tính rất quan trọng trong nhiều lĩnh vực, từ thiết kế máy móc đến nghiên cứu chuyển động của các vật thể trong vũ trụ, và đặc biệt là trong lĩnh vực [keyword].
Mô men Quán Tính: Định Nghĩa và Ý Nghĩa
Mô men quán tính, ký hiệu là I, là đại lượng đặc trưng cho khả năng chống lại sự thay đổi vận tốc góc của một vật đang quay quanh một trục. Giá trị của mô men quán tính càng lớn thì vật càng khó thay đổi vận tốc góc. Nó phụ thuộc vào khối lượng của vật và cách khối lượng đó phân bố xung quanh trục quay. [keyword] cũng chịu ảnh hưởng bởi mô men quán tính, việc tính toán chính xác giá trị này sẽ giúp tối ưu hóa hiệu suất và độ bền của [keyword].
Công thức Tính Mô men Quán Tính
Công thức chung để tính mô men quán tính của một vật gồm nhiều chất điểm là:
*I = Σ mi ri²**
Trong đó:
- mi là khối lượng của chất điểm thứ i
- ri là khoảng cách từ chất điểm thứ i đến trục quay
Đối với vật thể có phân bố khối lượng liên tục, công thức tính mô men quán tính được biểu diễn dưới dạng tích phân:
I = ∫ r² dm
Trong đó:
- dm là phần tử khối lượng
- r là khoảng cách từ phần tử khối lượng dm đến trục quay
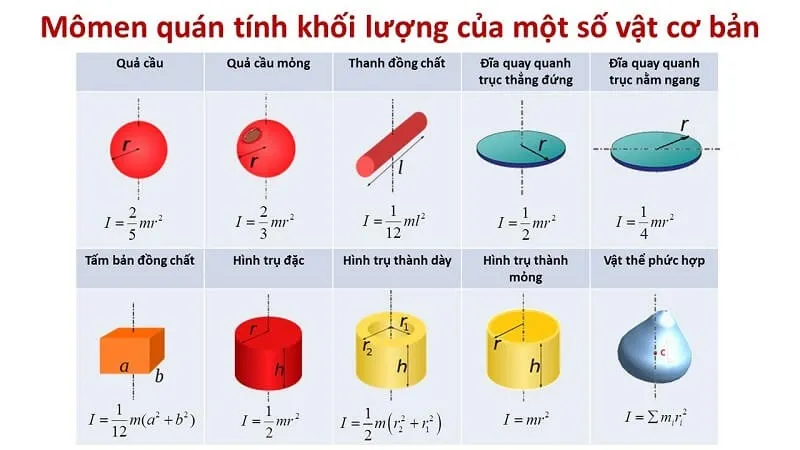
Dưới đây là công thức tính mô men quán tính cho một số vật thể phổ biến:
Hình tròn hoặc mặt trụ rỗng:
I = mR²
Trong đó: m là khối lượng vành tròn, R là bán kính.
Trụ đặc hoặc đĩa tròn mỏng:
I = (1/2)mR²
Mặt cầu rỗng:
I = (2/3)mR²
Khối cầu đặc:
I = (2/5)mR²
Hình trụ rỗng:
I = (1/2)M(R1² + R2²)
Trong đó: M là khối lượng hình trụ, R1 là bán kính trong, R2 là bán kính ngoài.
Vật thể dạng hình chữ nhật mỏng:
I = (1/12)m(a² + b²)
Trong đó: m là khối lượng, a và b là chiều dài và chiều rộng.
 Mô hình mô men quán tính
Mô hình mô men quán tính
Sau đoạn mở đầu, chèn liên kết nội bộ thứ nhất tại đây: Việc tính toán mô men quán tính rất quan trọng, đặc biệt khi xét đến lực xiết bu lông cường độ cao. Tại sao lực xiết bu lông cường độ cao rất quan trọng?
Định Lý Huygens-Steiner
Định lý Huygens-Steiner cho phép tính mô men quán tính của một vật đối với một trục quay bất kỳ, dựa vào mô men quán tính của vật đối với một trục song song đi qua trọng tâm của vật. Công thức được biểu diễn như sau:
I = Icm + md²
Trong đó:
- I là mô men quán tính đối với trục quay bất kỳ
- Icm là mô men quán tính đối với trục quay song song đi qua trọng tâm
- m là khối lượng của vật
- d là khoảng cách giữa hai trục quay
Ứng Dụng của Mô men Quán Tính
Mô men quán tính có nhiều ứng dụng quan trọng trong thực tế, bao gồm:
-
Thiết kế máy móc: Tính toán mô men quán tính giúp tối ưu hóa thiết kế các bộ phận quay như bánh răng, trục, và rotor. Điều này rất quan trọng đối với [keyword], giúp đảm bảo hoạt động hiệu quả và ổn định.
-
Kỹ thuật ô tô: Mô men quán tính ảnh hưởng đến khả năng tăng tốc và phanh của xe.
-
Robot: Kiểm soát mô men quán tính của các bộ phận robot giúp cải thiện độ chính xác và tốc độ của chúng.
-
Vật lý thiên văn: Mô men quán tính được sử dụng để nghiên cứu chuyển động quay của các hành tinh và các vật thể trong vũ trụ.
tụ máy bơm đóng vai trò quan trọng trong hệ thống bơm, và việc hiểu biết về mô men quán tính có thể giúp cải thiện hiệu suất và độ bền của tụ.
Kết luận
Mô men quán tính là một khái niệm quan trọng trong cơ học, đặc biệt là trong chuyển động quay. Hiểu rõ về mô men quán tính và cách tính toán nó giúp chúng ta thiết kế và vận hành các hệ thống cơ khí một cách hiệu quả hơn. Việc áp dụng kiến thức về mô men quán tính vào [keyword] có thể dẫn đến những cải tiến đáng kể về hiệu suất, độ bền và an toàn. Việc lựa chọn vật liệu và thiết kế hình dạng phù hợp cho [keyword] có thể tối ưu hóa mô men quán tính và cải thiện hiệu suất hoạt động. Quy cách thép V và các thông số cần thiết cũng là một yếu tố quan trọng cần xem xét khi thiết kế các cấu trúc liên quan đến [keyword].